We are very pleased to announce the 2012 major release of OrcaFlex, version 9.6. As always it takes time to produce and despatch installation CDs but clients with up-to-date MUS contracts can expect to receive the software in the first half of November. In fact we are thinking of switching to electronic distribution for future releases, which would mean that you would get the upgrade sooner after release.
The major enhancements introduced in 9.6 are as follows:
- 64 bit OrcaFlex
- New Line Contact model
- Full QTFs for wave drift
- Sum-frequency QTF loads
- Shear7 modes file generation for lines with torsion, Shear7 version 4.7
- P-y model improvements
- User defined results for external functions
As usual there are a large number of improvements to the program, far too many to discuss here. Full details can be found in the OrcaFlex help file.
What follows are brief introductions to the new features that we consider to be most significant.
64 bit OrcaFlex
Previous releases of OrcaFlex were 32 bit programs. Version 9.6 introduces 64 bit OrcaFlex. It’s perhaps not the most exciting development – it looks absolutely identical to 32 bit OrcaFlex! 64 bit Windows operating systems have been around since 2005, but only in the past few years have they become prevalent. One of the great features of 64 bit Windows is that it runs 32 bit programs exceedingly well. And, up until now, that’s how OrcaFlex has always been run on 64 bit Windows.
We are still supplying a 32 bit version of OrcaFlex. So version 9.6 comes with both 32 bit and 64 bit versions. By default, on a 64 bit system, the installation program will setup shortcuts for 64 bit OrcaFlex. But the 32 bit version will be installed and can be run if necessary. Files (i.e. data files, simulation files etc.) created by the 32 bit version can be read by the 64 bit version and vice versa.
We have not released a 64 bit version of OrcaFlex until now because our compiler vendor has not supported 64 bit Windows until quite recently. Fortunately there has been little need for 64 bit OrcaFlex. However, that is beginning to change. In particular the proliferation of multi-core and multi-processor machines is significant. A 32 bit process is limited in how much memory it can address – that limit is 4GB. Even if you have a machine with more memory, the 32 bit process can only see 4GB of it. This limitation can be restrictive for machines with a lot of processors and 64 bit OrcaFlex removes the restriction.
It would be nice to say that 64 bit OrcaFlex ran twice as fast as 32 bit OrcaFlex. Sadly that is not the case. 64 bit OrcaFlex is indeed a little faster than 32 bit OrcaFlex, but not very much. So the main benefit is breaking free of the constraints of 32 bit memory address space.
The other significant benefit relates to interfacing with other programs. Although 64 bit systems can run 32 bit processes, all the code inside a single process must be the same type. So a 64 bit process can only execute 64 bit code, and a 32 bit process can only execute 32 bit code. This means that if you have 32 bit Excel installed, then the OrcaFlex spreadsheet add-in must also be 32 bit. In the past that meant that you could not use the spreadsheet add-in with 64 bit Excel. Likewise, users of the Python and MATLAB interfaces had to install 32 bit versions of Python and MATLAB. With OrcaFlex 9.6, you can use OrcaFlex with either 32 bit or 64 bit versions of all these other programs. It’s not compulsory to update your existing Excel, Python or MATLAB installations to 64 bit. If there’s no pressing need to do it, don’t bother. We will carry on supporting 32 bit OrcaFlex for a long time to come.
New Line Contact model
You can now model contact between lines using a new Line Contact model. This new contact model is particularly suitable for modelling systems where:
- One line (or more than one) is inside another line, such as pipe-in-pipe systems and pull-in operations.
- One or more lines are constrained to follow another line at certain arc lengths, such as choke and kill lines on drilling risers, installation guide wires and piggy-back risers.
- A line strikes the outer surface of another, as seen in riser interference cases.
The line contact model supports relative axial motion between the contacting lines and can include axial friction.
This new line contact model is distinct from the previously existing line clashing model in OrcaFlex, which is still available.
The new contact model is a very significant development for OrcaFlex. It has been very challenging to implement, mainly because we have been very ambitious in the scope of the new contact model. The new model is extremely flexible and can be used to model a huge variety of scenarios. The challenge has been achieving this level of generality whilst maintaining the calculation robustness that our users expect. The new functionality has been on extended beta test with a number of OrcaFlex users and feedback has been very positive. We are very excited and proud of this new capability and hope that it proves useful and helpful to our users.
Full QTFs for wave drift
Previous versions of OrcaFlex modelled 2nd order wave drift loading using diagonal QTFs and the Newman approximation. The benefit of Newman’s approximation is one of computational efficiency. The full theory of 2nd order wave drift loading requires summation of loads due to all combinations of pairs of wave components. So if you have 10 wave components you need to sum 102 terms. If you have 100 wave components, you sum 1002 terms.
This double sum can be very expensive to evaluate. And that’s where Newman’s approximation comes into play. It uses an approximation to turn the double sum into a single sum over the wave components. That’s a great benefit in terms of efficiency, and the approximation is good so long as the water depth is deep. But in shallow water the approximation is poor.
To address that limitation we have implemented the full QTF double sum. The option of using the Newman approximation has been retained and there is a new option to use full QTFs instead. Full QTF data can be directly imported from either WAMIT or AQWA. If your data comes from a different source then you will need to pre-process it into a single table of values which can then be pasted into OrcaFlex.
Note that version 9.6a has disabled the option to import data from AQWA because we are as yet uncertain what phase conventions are used in the AQWA output file. We will resolve this in a minor 9.6 upgrade.
Sum frequency QTF loads
The implementation of full QTFs for wave drift loading made it easy for us to add sum frequency QTF loading. The input data for sum frequency QTF loads is identical to that for wave drift full QTFs. The difference comes in how the data are interpreted. Wave drift QTFs are based on difference frequencies whereas sum frequency QTFs are based on, as the name suggests, sum frequencies. Sum frequency QTF loading is used to model high frequency ringing on TLPs, for example.
Shear7 modes file generation for lines with torsion, Shear7 version 4.7
One of the key facilities that enables the OrcaFlex integration with the Shear7 VIV code is the ability to generate Shear7 modes files. In previous versions of the program, the creation of Shear7 modes files was limited to lines which did not model torsion. That covers the vast majority of cases and has not been a significant limitation. However, there are occasions when this limitation is inconvenient. So, for version 9.6, we have done the extra work required to allow modes files to be generated for lines with torsion.
Just before we completed work on version 9.6a, a new version of Shear7 was released, version 4.7. We did not have sufficient time to be able to update OrcaFlex to work with Shear7 4.7. However, we will do so over the next few weeks, and intend to include support for Shear7 4.7 in a minor update to 9.6.
P-y model improvements
OrcaFlex 9.5 introduced built-in P-y models. This feature has been very well received, but it had one glaring weakness – the program assumed that the undeformed configuration of the P-y springs was vertically upwards. For version 9.6 we have extended the functionality to cater for slightly off-vertical lines. The undeformed configuration of the P-y springs is determined by the end orientation at the bottom end of the line.
We have also added two new results variables associated with P-y models: P-y deflection and P-y resistance.
Finally, we have changed the implementation of the API RP 2A soft clay model to use the modified P-y table introduced in Supplement 3 to the code.
User-defined results for external functions
OrcaFlex has supported external functions for many years now. These external functions allow you to extend the OrcaFlex calculation algorithms using code of your own. Originally they had to be written using native code, typically C++, but version 9.5 added support for external functions written in Python.
One feature that has been requested for many years is the ability to define results variables when implementing external functions. For example, consider an external function that uses some intermediate values to calculate its returned value. In order to debug and understand the external function it is desirable to be able to see those intermediate values.
In version 9.5 we added the external function output window so that you could print debugging information to a text console. That’s a step forward but, as the saying goes, pictures speak a thousand words. So, in version 9.6 an external function can define results variables. These results variables are just like any other OrcaFlex results variables. They can be plotted as time histories, range graphs or XY graphs. They are available through all the post-processing interfaces that OrcaFlex exposes: Excel, Python, MATLAB, etc.
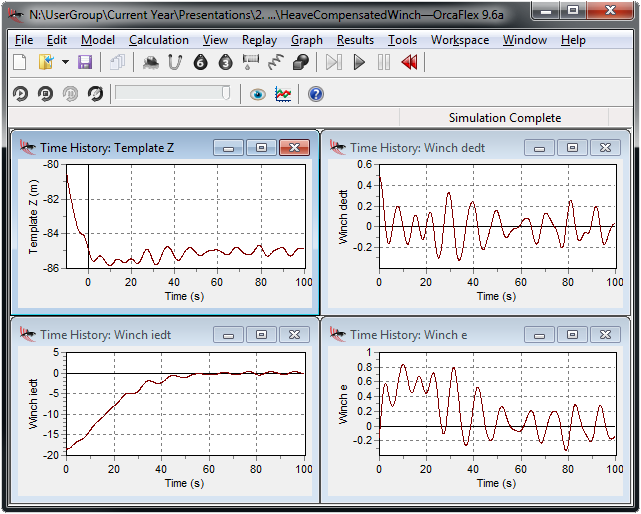
To illustrate, here’s a screenshot of our well-known active heave compensation example. This simulation models active heave compensation using an external function that implements a PID control system.
The Template Z plot shows the heave compensation system attempting to achieve a target value of -85m. The plots of the e, iedt and dedt results variables are, respectively, the proportional, integral and derivative parameters of the PID equation.
This is just one possible use for external function results. Since you are in full control of the external functions, you have the freedom to implement whatever you wish to.