
|
Constraints: Stiffness and damping |

|
Constraints: Stiffness and damping |
The constraint stiffness represents translational and rotational springs which resist displacement of the out-frame relative to the in-frame. The damping represents translational and rotational dampers which resist velocity of the out-frame relative to the in-frame.
| Note: | The same stiffness and damping model is applied to both Cartesian and curvilinear constraints. In the case of curvilinear constraints, this means that the stiffness and damping forces depend only upon the position and velocity of the out-frame relative to the in-frame, and not upon the particular choice of curvilinear coordinates that have been defined. The resultant loads will be resolved into components acting tangentially and normal to the constraint manifold in order to compute their effects upon the out-frame's motion and connection loads respectively. |
This determines how you will specify the stiffness and damping data. There are three choices:
This pertains to the calculation of rotational stiffness loads and is pertinent for all three stiffness and damping methods. The choice is available for directly solved Cartesian constraints with a single free rotational DOF. If rotational winding is enabled, then the angle of rotation, $\theta$, between the out-frame and the in-frame, is treated as unbounded (i.e. it can take any real value). This means that the stiffness moment continues to increase as the out-frame performs a full 360° rotation around the in-frame, and increases still further over each subsequent winding (e.g. $\theta$=720°, $\theta$=1080°, etc.). If rotational winding is not enabled, then $\theta$ is confined to lie within the primary range of -180° < $\theta \leq$ 180°. This means that a rotation of $\theta$ = 181° is treated as if it were a rotation of $\theta$ = -179° for purposes of the stiffness calculation.
| Note: | Owing to technical considerations, rotational winding is not permitted if the constraint solution method is indirect, or if the constraint is not Cartesian, or if there is more than one free rotational DOF. |
Stiffness and damping coefficients may be linear or nonlinear. Linear data are specified by a constant value that is interpreted as follows:
Nonlinear data are specified as variable data:
Nonlinear stiffness data can optionally be treated as hysteretic.
The stiffness and damping are isotropic, which means that each is the same in all directions, e.g. motion along the $x$-axis has the same stiffness as motion along the $y$-axis. Non-isotropic models can be constructed by connecting two or more constraint objects together in a chain, with different stiffness and damping data in each. For instance, the first constraint could specify a translational stiffness of 1kN/m with the $x$ DOF free, and the second constraint could specify a translational stiffness of 2kN/m with the $y$ DOF free.
Linear stiffness is defined by a single value, which applies to both positive and negative displacements.
Nonlinear stiffness, for a Cartesian constraint with a single free DOF, is double-sided. That is, the stiffness-displacement table should contain values of both positive and negative displacement. The values may be symmetrical about zero displacement, but do not have to be so (e.g. positive and negative displacements along the $x$-axis can give rise to different stiffnesses). This applies to the translational DOFs and the rotational DOFs separately and independently.
Nonlinear stiffness should otherwise be single-sided (with just positive displacements), for Cartesian constraints with more than one free translational DOF or more than one free rotational DOF, and for all curvilinear constraints. Why? Well because, for Cartesian constraints, it is not possible to unambiguously assign a sign to a displacement in more than one dimension without introducing discontinuities; for curvilinear constraints, there can be ambiguity even for one-dimensional motion (e.g. if the permitted motion of the out-frame does not pass through the origin of the in-frame).
Nonlinear stiffness variable data can optionally be treated as hysteretic. This is used to model non-elastic stiffness effects that depend upon the past history of the motion. The model used is directly analogous to the one used for line hysteretic bending. The independent variable in the line hysteretic bending model is curvature, whereas for constraints the independent variable is displacement or angular displacement; similarly, the dependent variable in the line model is bend moment, whereas for constraints it is stiffness force or moment. Hysteretic nonlinear stiffness data must always be single-sided, even in the case of a single free DOF, because the hysteresis model is not compatible with double-sided data.
| Warning: | For constraints with two or three rotational degrees of freedom, the hysteretic rotational stiffness model is strictly only valid for small angular displacements. It may not be appropriate in cases where the out-frame rotates significantly relative to the in-frame. As a rough guide, angular displacements of greater than 30° should be treated with caution, but this will vary on a case-to-case basis. |
Linear damping is defined by a single value, which applies to both positive and negative velocity. Positive velocity corresponds to increasing displacement between the in-frame and the out-frame.
Nonlinear translational damping data are two-sided: they can be specified for both positive and negative velocity. The translational damping here is analogous to that of spring-damper link objects. Imagine an invisible link connecting the in-frame to the out-frame. This link applies a stiffness force between the two frames in the usual way. However, the damping force does not resist the instantaneous relative velocity of the out-frame relative to the in-frame, but rather resists the rate of change of the magnitude of the displacement between the two frames (i.e. the rate of change of the length of the link) and acts along the line between the two frames. Motions of the out-frame that do not change the magnitude of the displacement between the two frames (i.e. perpendicular to the link) are therefore undamped. This assumption is made to provide consistency with OrcaFlex links and to avoid introducing additional moments between the in-frame and the out-frame.
Nonlinear rotational damping data are one-sided, with only positive values of relative angular velocity. The damping moment applied is proportional to the magnitude of the instantaneous angular velocity between the out-frame and the in-frame, in the direction opposing that angular velocity.
To be well-defined, stiffness and damping data should usually specify zero load at zero displacement (stiffness) and zero relative velocity (damping). The only exception to this rule is the case of Cartesian constraints with no more than a single translational DOF and no more than a single rotational DOF, for which (as above) it is possible to unambiguously define a non-zero stiffness force at zero displacement and angular displacement. However, the damping force must always be zero at zero relative velocity in all cases, without exception.
This option allows you to specify full 6×6 linear stiffness and damping matrices. Each 6×6 matrix can be decomposed into 4 3×3 blocks. For the stiffness matrix, $K$, these blocks have the following units: \begin{equation} \left[ \begin{matrix} \dfrac{F}{L} & \dfrac{F}{\rad} \\ \dfrac{FL}{L} & \dfrac{FL}{\rad} \end{matrix} \right] \end{equation} where $F$ and $L$ denote the units of force and length, respectively. For the damping matrix, $C$, the block units are: \begin{equation} \left[ \begin{matrix} \dfrac{F}{L/T} & \dfrac{F}{\rad/T} \\ \dfrac{FL}{L/T} & \dfrac{FL}{\rad/T} \end{matrix} \right] \end{equation} where $T$ denotes the unit of time. The stiffness force, $\vec{F}_\textrm{stiffness}$, and moment, $\vec{M}_\textrm{stiffness}$, are computed as follows: \begin{eqnarray} \vec{F}_\textrm{stiffness} &=& -K_\textrm{top-left} \, \vec{p}- K_\textrm{top-right} \vec{R} \\ \vec{M}_\textrm{stiffness} &=& -K_\textrm{bottom-left} \, \vec{p}- K_\textrm{bottom-right} \vec{R} \end{eqnarray} where $\vec{p} = (x, y, z)^\textrm{T}$ and $\vec{R} = (Rx, Ry, Rz)^\textrm{T}$, with $x$, $y$, $z$, $Rx$, $Ry$ and $Rz$ being the six internal constraint degrees of freedom. $\vec{R}$ has been written as a vector for convenience, although it really only behaves like one in the limit where its magnitude is vanishingly small.
The damping force, $\vec{F}_\textrm{damping}$, and moment, $\vec{M}_\textrm{damping}$, are computed as follows: \begin{eqnarray} \vec{F}_\textrm{damping} &=& -C_\textrm{top-left} \, \dot{\vec{p}} - C_\textrm{top-right} \vec{\omega} \\ \vec{M}_\textrm{damping} &=& -C_\textrm{bottom-left} \, \dot{\vec{p}} - C_\textrm{bottom-right} \vec{\omega} \end{eqnarray} where $\dot{\vec{p}}$ and $\vec{\omega}$ are, respectively, the out-frame velocity and angular velocity (relative and with respect to the in-frame).
$\vec{F}_\textrm{stiffness}$, $\vec{M}_\textrm{stiffness}$, $\vec{F}_\textrm{damping}$ and $\vec{M}_\textrm{damping}$ are load vectors defined with respect to the axes of the in-frame. They act directly on the out-frame, but also induce an equal and opposite reaction on the in-frame. This ensures that the total internal stiffness and damping load within the constraint is always zero.
The stiffness and damping loads calculated in this way are linear in the four quantities $\vec{p}$, $\vec{R}$, $\dot{\vec{p}}$ and $\vec{\omega}$. It is important to bear in mind that this linearity may not be appropriate when the separation between the in-frame and the out-frame becomes large.
A Python model allows you specify the stiffness and damping loads (acting between the in-frame and the out-frame) in terms of bespoke mathematical formulae. It is a Python variable data source with the following outputs and inputs:
F: the force applied to the out-frame by the in-frame.M: the moment applied to the out-frame by the in-frame.The components of F and M are defined with respect to the axes of the in-frame. The loads acting on the out-frame are automatically back-reacted onto the in-frame, to ensure that the total internal stiffness and damping loads within the constraint always sum to zero.
p: the position vector of the out-frame, relative and with respect to the in-frame; the three components of p are the internal translational degrees of freedom of the constraint, $x$, $y$ and $z$. p has been defined as a vector for convenience, to enable you to write basic vector equations in your Python equation script. The individual $x$, $y$ and $z$ components correspond to p[0], p[1] and p[2], respectively.R: an array containing the three internal rotational degrees of freedom of the constraint, $Rx$, $Ry$ and $Rz$.v: the velocity vector of the out-frame, relative and with respect to the in-frame. v is the time derivative of p.w: the angular velocity vector of the out-frame, relative and with respect to the in-frame.t: the simulation time.In addition, the following quantities can be used in your Python variable data equation script:
pMag: the magnitude of p; this is the distance between the in-frame and the out-frame.RMag: the magnitude of R; this is the angle of the axis-angle rotation vector that relates the out-frame to the in-frame.vMag: the magnitude of v; this is the speed of the out-frame relative to the in-frame.wMag: the magnitude of w; this is the angular speed of the out-frame relative to the in-frame.t0, the simulation time at the start of the simulation.rampStartTime, the simulation time at which the ramp becomes non-zero.rampFinishTime, the simulation time at which the ramp becomes equal to one.ramp, the current value of the ramping factor.rampDot, the first time derivative of the ramping factor.rampDotDot, the second time derivative of the ramping factor.intRamp, the time integral of the ramping factor.Python stiffness and damping models are illustrated by the following fun example, which has been set up to simulate the orbits of the planets around the Sun:
When you download and unzip the example, you will find two files: solarSystemParent.dat and solarSystem.yml, the second file restarting from the end of the first. The analysis contains nine 6D buoys to represent the Sun and the eight planets: Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus and Neptune. A technical explanation of the model set-up will be detailed below. For now, simply run both models and open the solarSystem.wrk workspace after the restart analysis has concluded. To gain the best view of the model, it is advisable to turn off the drawing of axes in the 3D view, and turn on the drawing of name labels and trails. When you do this, you will see that the planets orbit the Sun:
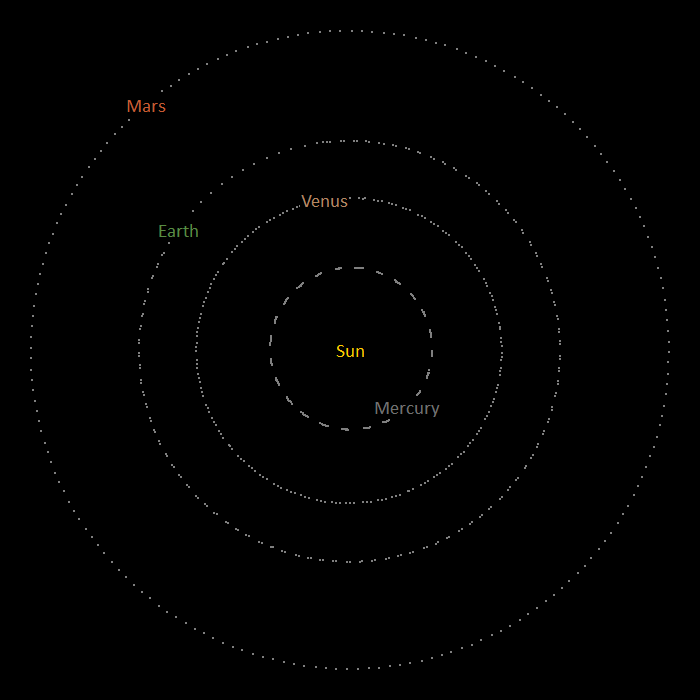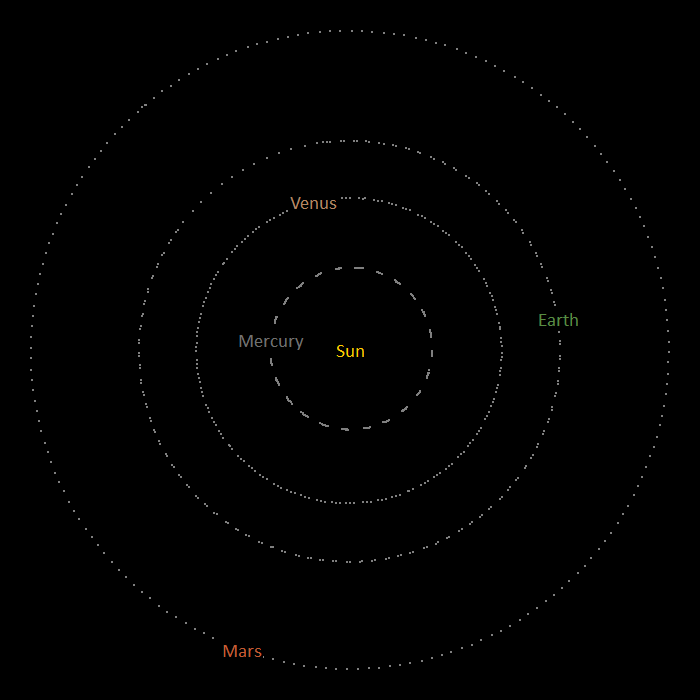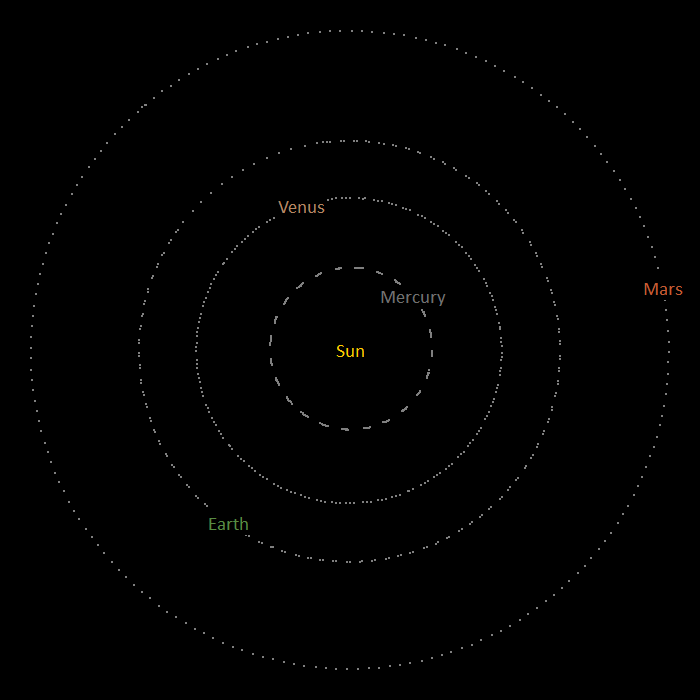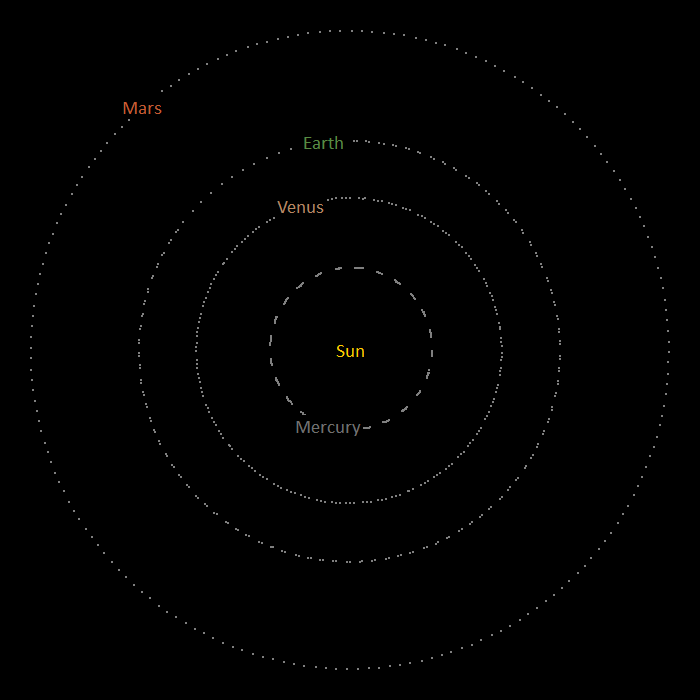
| Figure: | The motion of the inner planets |
| Note: | To make the replay easier to view, the physical properties of the model have been scaled so that 1000s of simulation time corresponds to one year of physical time. |
| The initial conditions (positions and velocities) of the planets are only approximate. The model has been created merely to demonstrate Python stiffness and damping models, and the resulting simulation is not expected to be a completely accurate representation of planetary motion. | |
| It looks as if the Sun is stationary in the above image; however, if you look closely in the 3D view, you will see that it actually moves. |
Notice that the orbital period of the Earth is approximately one year (1000s of simulation time). Let us now breakdown the constituent elements of the model:
The gravityModel stiffness and damping model has the following equation script:
This is a vector equation encoding Newton's law of gravity. This law states that the attractive gravitational force between two objects is directly proportional to the product of their masses, m1 and m2, and inversely proportional to the square of their separation, pMag. The constant of proportionality is G, the gravitational constant. In gravityModel, G, m1 and m2 have been defined as Python variable data constants, with the value of G having been adjusted to reflect the units system of the model, and the fact that time has been rescaled to condense one year of real time into 1000s of simulation time. The values of m1 and m2 are context-dependent and vary for each interacting pair of objects. G is universal, and takes the same value in all contexts.
This is just intended as a fun example to illustrate the utility of Python stiffness and damping models. In practice, this feature allows bespoke stiffness and damping models to be defined for a wide variety of applications where the coefficient and matrices methods have insufficient generality.